Postulat
Il est demandé ici seulement que chacun considère ses perceptions avec l’attention la plus diligente afin de pouvoir distinguer le clair de l’obscur.
Définitions
1. L’Étendue est ce qui comprend trois dimensions ; mais nous n’entendons pas par étendue l’acte de s’étendre ou quoi que ce soit de différent de la quantité.
2. Par Substance nous entendons ce qui n’a besoin pour exister que du seul concours de Dieu.
3. Un Atome est une partie de la matière indivisible de sa nature.
4. Indéfini est ce dont les limites (s’il en existe) ne peuvent être explorées par l’entendement humain.
5. Le Vide est l’étendue sans substance corporelle.
6. Entre l’Espace et l’étendue nous ne concevons qu’une distinction de raison, c’est-à-dire qu’il n’en est pas réellement distinct. Lire Principes, partie II, art. 10.
7. Nous appelons divisible au moins en puissance ce que nous connaissons par la pensée pouvoir être divisé.
8. Le mouvement dans l’espace est le transport d’une partie de la matière, c’est-à-dire d’un corps, du voisinage des corps qui le touchent immédiatement et sont considérés comme immobiles, dans le voisinage d’autres corps.
Descartes use de cette définition pour expliquer le mouvement dans l’espace ; pour la bien entendre il faut considérer :
1° Que par partie de la matière il entend tout ce qui peut être transporté à la fois, encore que cela même puisse être à son tour composé de beaucoup de parties ;
2° Que pour éviter la confusion dans cette définition, il parle seulement de ce qui est toujours dans la chose mobile, à savoir le transport, qui ne doit pas être confondu, comme il l’a été par d’autres, avec la force ou l’action qui transporte. On croit communément que cette force ou cette action est requise seulement pour le mouvement non pour le repos, en quoi l’on se trompe entièrement. Car, ainsi qu’il se connaît de soi, la même force qui est requise pour imprimer à un corps quelconque certains degrés de mouvement l’est aussi pour enlever à ce corps les mêmes degrés de mouvement, de façon qu’il vienne au repos. Cela est même prouvé par l’expérience, car il nous faut pour mettre en mouvement un navire au repos dans une eau stagnante une force à peu près égale à celle dont nous avons besoin pour l’arrêter brusquement quand il se meut ; et l’égalité serait assurément complète si nous n’étions aidés pour le retenir par la pesanteur et l’inertie de l’eau soulevée par le navire ;
3° Qu’il dit que le transport se fait du voisinage des corps contigus dans le voisinage d’autres corps, mais non d’un lieu dans un autre. Car le lieu (comme il l’a expliqué article 13, partie ll) n’est pas quelque chose de réel mais dépend seulement de notre pensée, de telle sorte que le même corps peut être dit à la fois changer et ne pas changer de lieu ; mais on ne peut dire qu’il est à la fois transporté et non transporté du voisinage d’un corps contigu ; car seuls certains corps déterminés peuvent être au même instant contigus au même corps mobile ;
4° Qu’il ne dit pas que le transport ait lieu absolument du voisinage des corps contigus, mais de ceux-là seulement qui sont considérés comme étant au repos. Pour qu’un corps A, en effet, soit transporté à distance d’un corps B, la même force est nécessaire d’un côté que de l’autre, ce qui apparaît clairement par l’exemple d’un bateau adhérant à la boue ou au sable qui sont au fond de l’eau ; pour qu’il en soit détaché il faut appliquer la même force au bateau et au fond. Pour cette raison la force qui doit mouvoir des corps se dépense également sur le corps mû et sur celui qui reste immobile. Voir Fig. 1.Le transport d’ailleurs est réciproque, car si le bateau est éloigné du sable, le sable aussi est éloigné du bateau. Si donc, parlant absolument, nous voulions attribuer des mouvements égaux dans des directions opposées à l’un comme à l’autre des deux corps qui se séparent, pour cette raison qu’il y a la même action dans l’un et dans l’autre, nous serions alors contraints d’attribuer tout autant de mouvement aux corps considérés comme immobiles, par exemple au sable duquel le bateau est détaché, qu’aux corps mûs ; car, ainsi que nous l’avons montré, la même action est requise des deux côtés et le transport est réciproque. Mais cela serait se trop écarter de la façon commune de parler. Toutefois, bien que ces corps desquels les autres sont séparés, soient considérés comme immobiles et ainsi dénommés, nous nous rappellerons cependant que tout ce qui est dans le corps mû, à cause de quoi il est dit se mouvoir, est aussi dans le corps immobile.
5° Enfin il apparaît clairement par cette Définition que chaque corps a seulement un mouvement qui lui soit propre parce qu’on le conçoit comme s’éloignant seulement de certains corps déterminés à lui contigus et immobiles. Toutefois, si le corps mû est une partie d’autres corps ayant d’autres mouvements, nous connaissons clairement qu’il peut avoir part à des mouvements innombrables ; mais comme il n’est pas facile d’en concevoir à la fois une telle quantité et que tous ne peuvent même pas dire reconnus, il suffira de considérer dans chaque corps cet unique mouvement qui lui est propre (Voir Principes, partie II, art. 31).
9. Par cercle de corps mûs nous entendons seulement ce qui se produit quand le dernier corps mû par l’impulsion d’un autre est immédiatement contigu au premier, encore que la figure formée par tous les corps sous l’impulsion d’un même mouvement soit très sinueuse. Voir Fig. 2.
Axiomes
1. Le néant n’a pas de propriétés.
2. Rien de ce qui peut être enlevé d’une chose sans porter atteinte à son intégrité ne constitue son essence ; mais ce qui, s’il est enlevé, supprime la chose, constitue son essence.
3. Sur la dureté le sens ne nous apprend rien et nous n’en pouvons rien connaître clairement et distinctement, sinon que les parties des corps durs résistent au mouvement de nos mains.
4. Si deux corps se rapprochent ou s’éloignent l’un de l’autre, ils n’occuperont pas pour cela un espace plus grand ou plus petit.
5. Une partie de la matière, soit qu’elle cède, soit qu’elle résiste, ne perd pas pour cela la nature d’un corps.
6. Le mouvement, le repos, la figure et autres choses semblables ne peuvent être conçus sans l’étendue.
7. En sus des qualités sensibles, il ne reste rien, dans un corps, que l’étendue et ses affections énumérées dans la première partie des Principes.
8. Un même espace, ou une étendue quelconque, ne peut être plus grand une fois qu’une autre.
9. Toute étendue peut être divisée au moins par la pensée.
La vérité de cet Axiome ne paraîtra douteuse à aucune personne ayant appris les éléments de la Mathématique. Car l’espace donné entre la Tangente et le Cercle peut toujours être divisé par une infinité de Cercles plus grands. La même chose se voit par le moyen des Asymptotes d’une Hyperbole.
10. Personne ne peut concevoir les limites d’une étendue ou d’un espace qu’il ne conçoive au delà de ces limites d’autres espaces suivant immédiatement le premier.
11. la matière est multiple et qu’une matière ne touche pas l’autre immédiatement, chacune est comprise sous les limites au delà desquelles il n’y a plus de matière.
12. Des corps très petits cèdent facilement au mouvement de nos mains.
13. Un espace ne pénètre pas un espace et n’est pas plus grand une fois qu’une autre.
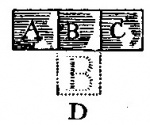
14. Si un canal A est de même longueur qu’un autre C et C deux fois plus large que A, et si quelque matière fluide passe deux fois plus vite à travers le canal A que celle qui passe à travers le canal C, autant de masse passera dans le même espace de temps à travers le canal A qu’à travers le canal C. Et si autant de matière passe à travers le canal A qu’à travers C, celle qui passe à travers A aura une vitesse double. Voir Fig. 3.
15.Des choses qui s’accordent avec une même troisième s’accordent entre elles. Et celles qui sont doubles d’une même troisième sont égales entre elles. 16.Une matière qui est mue de diverses façons, a au moins autant de parties séparées actuellement les unes des autres qu’on y peut observer en même temps de degrés différents de vitesse.
17. La ligne la plus courte entre deux points est la droite.
18. Le corps A qui se meut de C vers B, s’il est repoussé par une impulsion en sens contraire, se mouvra selon la même ligne vers C. Voir Fig. 4.
19. Des corps qui ont des mouvements opposés, quand ils viennent à se rencontrer, doivent éprouver l’un et l’autre quelque changement, ou au moins l’un des deux.
20. Un changement dans une chose provient d’une force plus grande.
21. Si, quand le corps 1 se meut vers le corps 2 et le pousse, le corps 8 par cette impulsion est mû vers 1, les corps 1, 2, 3 ne peuvent être en ligne droite, mais tous jusqu’à 8 forment un cercle complet.
Lemme 1
Où il y a de l’Étendue ou de l’Espace il y a nécessairement une substance.
Démonstration : L’étendue ou l’espace (par l’Axiome 1) ne peut être un pur néant ; elle est donc un attribut qui doit nécessairement appartenir à quelque chose. Ce n’est pas à Dieu (par la Proposition 16, partie I) ; c’est donc à une chose qui n’a besoin pour exister que du seul concours de Dieu (par la Proposition 12, partie I), c’est-à-dire à une substance (par la Définition 2, partie II). C.Q.F.D.
Lemme 2
La Raréfaction et la Condensation sont conçues clairement et distinctement par nous bien que nous n'accordions pas que les corps occupent dans la raréfaction un espace plus grand que dans la condensation.
Démonstration : La raréfaction et la condensation se peuvent concevoir en effet par cela seul que les parties d'un corps s'écartent ou se rapprochent les unes des autres, donc (par l'Axiome 4) elles n'occuperont un espace ni plus grand ni plus petit. Car, si les parties d'un corps, supposons d'une éponge, par cela seul qu'elles se rapprochent les unes des autres expulsent les corps qui remplissaient les intervalles les séparant ; par cela même ce corps deviendra plus dense, et cependant ses parties n'occuperont pas un espace plus grand qu'auparavant (par l'Axiome 4). Et, si elles s'écartent de nouveau les unes des autres et que les cavités se remplissent d'autres corps, il y aura raréfaction et cependant les parties n'occuperont pas un espace plus grand. Et cela, qu'à l'aide des sens nous percevons clairement dans l'éponge, nous pouvons le concevoir, par le seul entendement, de tous les corps, bien que les intervalles des parties échappent entièrement au sens de l'homme. Donc la Raréfaction et la Condensation sont conçues clairement et distinctement par nous bien que, etc. C.Q.F.D.
Il a paru bon de placer en tête ces lemmes pour débarrasser l'entendement de ses préjugés sur l'Espace, la Raréfraction, etc., et le rendre apte à entendre ce qui suivra.
Proposition 1
Encore que l'on enlève d'un corps la dureté, le poids et les autres qualités sensibles, la nature de ce corps n'en gardera pas moins son intégrité.
Démonstration : Sur la dureté le sens ne nous apprend rien et nous n'en pouvons rien concevoir clairement et distinctement, sinon que les parties des corps durs résistent au mouvement de nos mains (par l'Axiome 3). Donc (par la Proposition 14, partie I), la dureté ne sera rien d'autre. Or, si l'on divise le corps dur en poussière aussi menue que possible, ses parties céderont facilement (par l'Axiome 12), et cependant ne perdront pas la nature d'un corps (par l'Axiome 5). C. Q. F. D.
Au sujet du poids et des autres qualités sensibles la démonstration a lieu de la même façon.
Proposition 2
La nature du Corps, autrement dit de la matière consiste dans la seule étendue.
Démonstration : La nature du corps n'est pas détruite par l'enlèvement des qualités sensibles (par la Proposition 1, partie II) ; donc elles ne constituent pas son essence (par l'Axiome 2). Rien ne reste donc que l'étendue et ses affections (par l'Axiome 7). Donc, si l'étendue est enlevée, rien ne restera qui appartienne à la nature du corps, mais elle sera entièrement détruite ; donc (par l'Axiome 2) la nature du corps consiste dans la seule étendue. C.Q.F.D.
Corollaire : L'Espace et le Corps ne diffèrent pas réellement.
Démonstration : Le corps et l'étendue ne diffèrent pas réellement (par la Proposition précédente) ; l'espace et l'étendue (par la Définition 6), ne diffèrent pas non plus réellement ; donc (par l'Axiome 15) l'espace et le corps ne diffèrent pas réellement. C.Q.F.D.
Scolie : Bien que nous disions[1] que Dieu est partout il n'est pas accordé par là que Dieu soit étendu ; c'est-à-dire (par la Proposition précédente) corporel ; car cette ubiquité se rapporte à la seule puissance de Dieu et à son concours par lequel toutes choses sont conservées ; de sorte que l'ubiquité de Dieu ne se rapporte pas plus à une étendue ou à un corps qu'à des anges ou à des âmes humaines. Mais il est à noter que, lorsque nous disons que sa puissance est partout, nous n'en séparons pas son essence ; car où est sa puissance est aussi son essence (Proposition 17, Corollaire partie I) ; mais excluons seulement toute corporéité, c'est-à-dire que Dieu n'est pas partout par quelque puissance corporelle, mais par une puissance ou essence divine, servant également à la conservation de l'étendue et à celle des choses pensantes (Proposition 17, partie I) qu'il ne pourrait certainement pas conserver si sa puissance, c'est-à-dire son essence, était corporelle.
Proposition 3
Il répugne qu'il existe un vide.
Démonstration : On entend par vide une étendue sans substance corporelle (par la Définition 5), c'est-à-dire (par la Proposition 2, partie II) un corps sans corps, ce qui est absurde.
Pour plus ample explication et pour corriger le préjugé relatif au vide, qu'on lise les articles, 17 et 18 de la partie II des Principes, où l'on observera principalement que des corps entre lesquels rien n'est interposé se touchent nécessairement l'un l'autre et aussi que le néant n'a point de propriétés.
Proposition 4
Une même partie d’un corps n'occupe pas un plus grand espace une fois qu'une autre fois et, inversement, le même espace ne contient pas plus de corps une fois qu'une autre fois.
Démonstration : L'espace et le corps ne diffèrent pas réellement (par le Corollaire de la Proposition 2, partie II). Donc, quand nous disons qu'un espace n'est pas plus grand une fois qu'une autre (par l'Axiome 13), nous disons aussi qu'un corps ne peut pas être plus grand, c'est-à-dire occuper un espace plus grand, une fois qu'une autre. Ce qui était le premier point à démontrer. Maintenant, de ce que l'espace et le corps ne diffèrent pas réellement, il suit qu'en disant qu'un corps ne peut occuper un espace plus grand une fois qu'une autre fois, nous disons du même coup que le même espace ne peut occuper plus de corps une fois qu'une autre fois. C. Q. F. D.
Corollaire : Des corps qui occupent même espace, supposons de l'or et de l'air, contiennent une égale quantité de matière ou de substance corporelle.
Démonstration : La substance corporelle ne consiste pas dans la dureté, par exemple la dureté de l'or, ni dans la mollesse, par exemple la mollesse de l'air, ni dans aucune des qualités sensibles (par la Proposition 1, partie II), mais dans la seule étendue (par la Proposition 2, partie II). Comme d'ailleurs (par hypothèse) il y a autant d'espace, c'est-à-dire d'étendue (par la Définition 6), dans l'un que dans l'autre, il y aura donc autant de substance corporelle. C. Q. F. D.
Proposition 5
Il n'existe point d'Atomes.
Démonstration : Les Atomes sont des parties indivisibles de leur nature (par la Définition 3). Mais, comme la nature de la matière consiste dans l'étendue (par la Proposition 2, partie II) qui, de sa nature est divisible, si petite qu'elle soit (par l'Axiome 9 et la Définition 7), une partie de la matière, si petite qu'elle soit, sera donc divisible de sa nature, c'est-à-dire qu'il n'existe point d'Atomes ou de parties de la matière indivisibles de leur nature. C.Q.F.D.
Scolie : La question des atomes fut toujours difficile et embrouillée. Quelques-uns affirment qu'il y a des Atomes parce qu'un infini ne peut être plus grand qu'un autre infini ; or si deux quantités, disons A et une quantité double de A, sont divisibles à l'infini, elles pourront aussi par la puissance de Dieu, qui connaît leurs parties infinies d'une seule vue, être actuellement divisées en parties infinies. Donc, puisqu'un infini ne peut être, ainsi que nous l'avons dit, plus grand qu'un autre infini, la quantité A sera égale à une quantité double, ce qui est absurde. On demande en outre si la moitié d'un nombre infini est aussi infinie, si elle est paire ou impaire, et autres questions semblables. A tout cela Descartes répond que nous ne devons pas rejeter les choses qui tombent sous notre entendement et sont conçues par suite clairement et distinctement, à cause d'autres choses qui dépassent notre entendement ou notre compréhension et par suite ne peuvent pas être perçues par nous sinon très inadéquatement. Or l'infini et ses propriétés dépassent l'entendement humain, lequel est de sa nature fini ; il serait donc inepte de rejeter comme faux ce que nous concevons clairement et distinctement au sujet de l'espace, ou de le tenir pour douteux, parce que nous ne comprenons pas l'infini. Et pour cette raison Descartes tient pour indéfinies ou illimitées les choses dans lesquelles nous n'observons point de limites, comme l'étendue du monde, la divisibilité des parties de la matière, etc. Lire les Principes, partie 1, article 26.
Proposition 6
La matière est indéfiniment étendue, et la matière du ciel et de la terre est une et la même.
Démonstration :
1° Démonstration de la première partie : Nous ne pouvons imaginer nulles limites de l'étendue, c'est-à-dire (par la Proposition 2, partie II) de la matière, sans concevoir au delà de ces limites d'autres espaces suivant immédiatement (par l'Axiome 10), c'est-à-dire (par la Définition 6) de l'étendue ou encore de la matière et cela indéfiniment. Ce qu'il fallait démontrer en premier.
2° Démonstration de la deuxième partie : l'essence de la matière consiste dans l'étendue (par la Proposition 2, partie II), et elle est indéfinie (par la première partie de celle Démonstration), c'est-à-dire (par la Définition 4) qu'elle ne peut être perçue sous aucunes limites par l'entendement humain ; donc (par l'Axiome 11) elle n'est pas multiple, mais une et la même partout. Ce qui était le second point.
Scolie : Nous avons traité jusqu'ici de la nature ou essence de l'étendue. Que d'ailleurs, elle existe, créée par Dieu, telle que nous la concevons, nous l'avons démontré dans la Proposition dernière de la partie I ; et il suit de la Proposition 12 de la partie I, qu'elle est conservée maintenant par la même puissance qui l'a créée. En outre, dans cette même Proposition dernière de la partie I, nous avons démontré que nous, en tant que choses pensantes, étions unis à une certaine partie de cette matière et que, par son aide, nous percevons l'existence actuelle de tous ces changements dont, par la seule contemplation de la matière, nous la savons capable ; ainsi la divisibilité, le mouvement dans l'espace, c'est-à-dire le passage d'une partie d'un lieu dans un autre, passage dont nous avons une idée claire et distincte, pourvu que nous connaissions que d'autres parties de la matière viennent prendre la place de celles qui ont été déplacées. Cette division de la matière et ce mouvement sont conçus par nous d'une infinité de manières et, par suite, une infinité de changements de la matière peuvent être conçus. Je dis qu'ils sont conçus par nous clairement et distinctement, tant que nous les concevons comme des modes de l'étendue, mais non comme des choses réellement distinctes de l'étendue, ainsi qu'il a été amplement expliqué dans la première partie des Principes. Et bien que les Philosophes aient forgé d'autres mouvements*, nous, qui n'admettons rien que nous ne concevions clairement et distinctement, nous n'admettrons d'autre mouvement que le mouvement dans l'espace parce que nous connaissons clairement et distinctement que l'étendue n'est capable d'aucun autre et que même aucun autre ne tombe sous notre imagination.
Zénon cependant, à ce qu'on rapporte, a nié le mouvement dans l'espace, et cela pour diverses raisons que Diogène le Cynique a réfutées à sa manière en marchant dans l'école où enseignait Zénon et en troublant ses auditeurs. Quand il sentit qu'un d'eux le retenait pour l'empêcher de marcher, il l'apostropha en ces termes : « Comment oses-tu réfuter les raisonnements de ton maître ? » Pour que nul cependant, trompé par les raisonnements de Zénon, ne croie que les sens nous font voir quelque chose — à savoir le mouvement — qui contredise entièrement à l'entendement, de telle sorte que l'esprit serait trompé même au sujet des choses qu'il perçoit clairement et distinctement à l'aide de l'entendement, je reproduirai ici les principaux raisonnements de Zénon, et je montrerai en même temps qu'ils ne s'appuient que sur de faux préjugés, c'est-à-dire que ce philosophe n'avait aucun concept vrai de la matière.
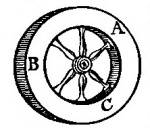
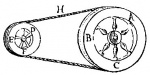
En premier lieu, il aurait dit que, s'il existait un mouvement dans l'espace, le mouvement d'un corps mû circulairement avec la plus grande célérité ne différerait pas du repos ; or, cette conséquence est absurde ; donc aussi la supposition d'où on la tire. Il prouve ainsi cette conséquence. Un corps est au repos, quand tous les points demeurent constamment en un même lieu ; or, tous les points d'un corps mû circulairement avec la plus grande vitesse demeurent constamment en un même lieu. Donc, etc. Et cela même, il l'aurait expliqué par l'exemple d'une roue, disons ABCD. Si cette roue se meut autour de son centre avec une certaine vitesse, le point A décrira un cercle par B et C plus rapidement que si la roue se mouvait plus lentement. Supposons donc, par exemple, quand elle commence lentement à se mouvoir que le point A revienne au bout d'une heure à son lieu de départ. Si la vitesse est supposée double, il reviendra à son lieu de départ au bout d'une demi-heure, et, si on la suppose quadruple, au bout d'un quart d'heure ; et, si nous concevons que cette vitesse augmente à l'infini et que le temps de la rotation diminue jusqu'à l'instantanéité, alors le point A, dans cette plus grande vitesse, sera à tous les instants, c'est-à-dire constamment dans son lieu de départ et ainsi demeure toujours en un même lieu. Ce que nous connaissons du point A doit d'ailleurs être entendu de tous les points de la roue ; et ainsi tous ces points dans cette plus grande vitesse seront constamment dans un même lieu. Pour répondre, il faut observer que cet argument porte plutôt contre une vitesse supposée la plus grande que contre le mouvement lui-même ; nous n'examinerons cependant point ici si Zénon argumente correctement mais plutôt les préjugés sur lesquels s'appuie toute cette argumentation, en tant qu'elle prétend combattre le mouvement. En premier lieu, donc il suppose que les corps peuvent être conçus comme se mouvant avec une vitesse telle qu'ils ne puissent pas se mouvoir plus vite. En second lieu, il compose le temps d'instants comme d'autres ont conçu que la quantité est composée de points indivisibles. L'une et l'autre suppositions sont fausses. Car, d'abord, nous ne pouvons jamais concevoir un mouvement si rapide que nous n'en concevions en même temps un plus rapide ; et, en effet, il répugne à notre entendement de concevoir un mouvement, quelque petite que soit la ligne décrite, si rapide qu'il n'en puisse exister de plus rapide. Et il en est de même à l'égard de la lenteur car il implique contradiction de concevoir un mouvement si lent qu'il n'en puisse exister de plus lent. Nous affirmons encore la même chose du temps, qui est la mesure du mouvement, c'est-à-dire qu'il répugne clairement à notre entendement de concevoir un temps tel qu'il n'en puisse exister de plus court. Pour prouver tout cela, suivons les traces de Zénon. Supposons donc comme lui une roue ABC se mouvant autour de son centre avec une vitesse telle que le point A soit à tous les instants dans le lieu A d'où il part. Je dis que je conçois clairement une vitesse indéfiniment plus grande et, par conséquent, des instants plus petits à l'infini ; que l'on suppose en effet, tandis que la roue ABC tourne autour de son centre, qu'à l'aide d'une corde H une autre roue DEF (je la suppose deux fois plus petite) soit elle-même mise en mouvement autour de son centre. Comme la roue DEF est supposée deux fois plus petite que ABC, il est clair que cette roue DEF se mouvra deux fois plus vite que la roue ABC et, par conséquent, que le point D se, retrouvera dans le lieu d'où il part au bout d'instants deux fois plus petits. Ensuite, si nous attribuons à la roue ABC le mouvement de la roue DEF, alors DEF se mouvra quatre fois plus vite qu'auparavant [ABC] ; et si de nouveau nous attribuons à ABC cette vitesse de DEF, alors DEF se mouvra huit fois plus vite, et ainsi à l'infini. Mais cela se voit déjà par le seul concept de la matière. Car l'essence de la matière consiste dans l'étendue ou l'espace, toujours divisible, comme nous l'avons prouvé ; et il n'y a pas de mouvement sans espace. Nous avons démontré aussi qu'une même partie de la matière ne peut pas occuper en même temps deux espaces, ce qui serait la même chose que de dire qu'une même partie de la matière égale une quantité double d'elle-même, comme il est évident par ce qui a été démontré ci-dessus. Donc, si une partie de la matière est en mouvement, elle se meut dans un certain espace et cet espace, si petit qu'on le suppose, sera cependant divisible et par conséquent aussi le temps par lequel cet espace est mesuré ; et par suite la durée ou le temps de ce mouvement sera aussi divisible et cela à l'infini.C.Q.F.D.
Passons maintenant à un autre sophisme, attribué au même Zénon, qui s’énonce comme il suit. Si un corps est en mouvement, ou bien il se meut dans le lieu où il est, ou bien dans le lieu où il n’est pas. Or ce n’est pas dans le lieu où il est, car, s’il est quelque part, il est nécessairement immobile. Ce n’est pas non plus dans le lieu où il n’est pas. Donc ce corps ne se meut pas. Mais cette argumentation est toute semblable à la précédente ; car on suppose qu’il existe un temps tel qu’il n’y en ait pas de plus petit. - Si en effet nous répondons à Zénon que le corps se meut non dans un lieu mais du lieu où il est au lieu où il n’est pas, il nous demandera ; ce corps n’a-t-il pas été dans les lieux intermédiaires ? - Si nous répondons par cette distinction : Entendez-vous par ces mots il a été, qu’il est demeuré en repos, nous nions qu’il ait été nulle part aussi longtemps qu’il était en mouvement ; si il a été signifie qu’il a existé nous disons qu’il existait nécessairement pendant le temps qu’il se mouvait ; Zénon demandera alors : Où a-t-il existé pendant le temps qu’il se mouvait ? - Si nous répondons derechef : demandez-vous par ces mots où a-t-il existé, en quel lieu s’est-il tenu pendant qu’il était en mouvement, nous répondrons qu’il ne s’est tenu en aucun lieu pendant qu’il se mouvait ; mais, si vous demandez quel lieu il a abandonné, nous dirons qu’il a abandonné tous les lieux que l’on voudra assigner dans l’espace qu’il a parcouru, Zénon demandera s’il a pu à un même instant du temps occuper un lieu et l’abandonner ? - A quoi nous répondons par cette distinction nouvelle : si par un instant du temps vous entendez un temps tel qu’il n’en puisse exister de plus petit, c’est demander une chose qui ne peut s’entendre, comme nous l’avons assez montré, et qui, par suite, ne mérite pas de réponse ; si le temps se prend au sens que j’ai expliqué plus haut, c’est-à-dire dans son vrai sens, on ne pourra, jamais assigner de temps si petit que, même en le supposant indéfiniment plus court, un corps ne puisse pendant ce temps et occuper et abandonner un lieu ; chose manifeste pour qui est assez attentif. On voit par là clairement, ce que nous disions plus haut, que Zénon suppose un temps si petit qu’il n’en puisse exister de plus petit, et que, par suite, il ne prouve rien.
Outre ces deux arguments, on rapporte de Zénon un autre argument qui se peut lire avec sa réfutation dans Descartes : Lettre avant-dernière du premier volume des Lettres.
Je désire cependant que mes lecteurs observent ici qu’aux raisonnements de Zénon j’ai opposé des raisonnements ; et ainsi je l’ai réfuté par la Raison et non par les sens, comme l’a fait Diogène. Jamais en effet les sens ne peuvent fournir à l’homme cherchant la vérité, que des Phénomènes de la Nature par lesquels il est déterminé à la recherche de leurs causes ; ils ne peuvent lui fournir quoi que ce soit qui montre la fausseté de ce que l’entendement reconnaît clairement et distinctement être vrai. C’est ainsi que nous jugeons, et c’est là notre Méthode ; démontrer les choses que nous proposons par des raisons que l’entendement perçoive clairement et distinctement ; tenant pour négligeable ce que les sens peuvent dire qui leur paraît contraire. Ainsi que nous l’avons dit en effet, ils peuvent déterminer seulement l’entendement à chercher ceci plutôt que cela, mais non le convaincre de fausseté quand il a perçu quelque chose clairement et distinctement.
Proposition 7
Nul corps ne peut prendre la place d'un autre, que cet autre ne prenne lui-même la place d'un autre.
Démonstration : Si on le nie qu'on suppose, s'il est possible, qu'un corps A[2] prenne la place d'un corps B, que je suppose égal à A et ne quittant pas sa place. L'espace alors qui contenait seulement B contient (par hypothèse) A et B ; c'est-à-dire le double de la substance corporelle qu'il contenait auparavant ; ce qui (par la Proposition 4, partie II) est absurde. Donc aucun corps ne prend la place d'un autre, etc. C.Q.F.D.
Proposition 8
Quand un corps prend la place d'un autre, au même instant du temps le lieu abandonné par lui est occupé par un autre corps qui le touche immédiatement.
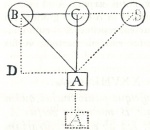
Démonstration : Si le corps B se meut vers D, les corps A et C au même instant du temps s'approcheront l'un de l'autre et se toucheront, ou bien ils n'en feront rien. S'ils se rapprochent l'un de l'autre et se touchent, notre proposition est reconnue vraie.
S'ils ne se rapprochent pas l'un de l'autre, mais que tout l'espace abandonné par B continue de séparer A de C, c'est donc qu'un corps égal à B (par le Corollaire de la Proposition 2 et le Corollaire de la Proposition 4, partie II) est situé entre eux. Mais ce corps n'est pas B (par hypothèse) ; c'est donc un autre qui au même instant du temps prend la place de B, et, comme il la prend au même instant du temps, il ne peut être autre qu'un corps qui touche B immédiatement (par le Scolie de la Proposition 6 de cette partie) ; car, nous l'avons démontré là, il n'existe pas de mouvement d'un lieu à un autre qui ne requière un temps lequel ne sera jamais si petit qu'il n'en puisse exister de plus petit. D'où il suit que la place du corps B ne peut au même instant du temps être occupée par un autre corps qui devrait parcourir un certain espace avant de l'occuper. Donc seul un corps qui touche B immédiatement prend sa place à l'instant même.Scolie : Puisque les parties de la matière sont réellement distinctes les unes des autres (par l'Article 61, partie I des Principes), l'une peut être sans l'autre (par le Corollaire de la Proposition 7, partie I) et elles ne dépendent pas les unes des autres. C'est pourquoi toutes les fictions sur la Sympathie et l'Antipathie doivent être rejetées comme fausses. En outre, comme la cause d'un certain effet doit toujours être positive, on ne devra jamais dire qu'un corps est mû pour qu'il n'y ait pas de vide, mais seulement, qu'il est mû par l'impulsion qu'il reçoit d'un autre.
Corollaire : En tout mouvement il y a toujours un cercle complet de corps mûs en même temps.
Démonstration : Dans le temps que le corps 1 occupe la place du corps 2, ce corps 2 doit occuper la place d'un autre, disons 3 et ainsi de suite (par la Proposition 7, partie II). En outre, au même instant du temps où 1 prend la place de 2 le lieu abandonné par 1 doit être occupé par un autre (par la Proposition 8, partie II) ; disons , 8 ou un autre qui touche 1 immédiatement. Or, puisque cela a lieu par la seule impulsion d'un autre corps (par le Scolie de la Proposition précédente), que l'on suppose ici être 1, tous ces corps ne peuvent pas se mouvoir en ligne droite (par l'Axiome 21) mais (par la Définition 9) forment un cercle complet (Voir fig. 2).Proposition 9
Si un canal circulaire ABC est plein d'eau et qu'il soit en A quatre fois plus large qu'en B, dans le temps que l'eau (ou tout autre corps fluide) qui est en A commence à se mouvoir vers B, l'eau qui est en B se mouvra quatre fois plus vite.
Démonstration : Puisque toute l'eau qui est en A se meut vers B, une quantité égale venant de C qui touche A immédiatement doit prendre sa place (par la Proposition 8, partie II) ; et, venant de B, une quantité d'eau égale doit occuper la place C (par la même Proposition) ; donc (par l'Axiome 14), cette quantité se mouvra quatre fois plus vite.C.Q.F.D.
Ce que nous disons d'un canal circulaire doit s'entendre aussi de tous les espaces inégaux par où des corps qui se meuvent ensemble sont obligés de passer ; la démonstration sera la même dans les autres cas.
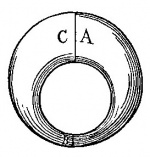
Lemme : Si deux demi-cercles sont décrits du même centre comme A et B, l'espace compris entre les périphéries sera partout le même ; mais si deux demi-cercles sont tracés de centres différents comme C et D, l'espace compris entre les périphéries sera partout différent. La démonstration découle évidemment de la seule définition du cercle.
Proposition 10
Un corps fluide qui se meut à travers un canal ABC reçoit des degrés de vitesse en nombre illimité.
Démonstration : (Voir la figure de la Proposition précédente.) L'espace entre A et B est partout différent (par le Lemme précédent) ; donc (par la Proposition 9, partie II), la vitesse avec laquelle le corps fluide se meut dans le canal ABC est partout différente. De plus, comme entre A et B, nous pouvons concevoir par la pensée une infinité d'espaces de plus en plus petits (par la Proposition 5, partie II), nous concevons aussi en nombre illimité les inégalités qui sont partout et, par suite (par la Proposition 9, partie II), il y aura des degrés de vitesse en nombre illimité. C.Q.F.D.
Proposition 11
Dans une matière qui coule par le canal ABC, il y a une division en particules illimitées en nombre.
Démonstration :
(Voir la figure de la Proposition 9.) La matière qui coule par le canal ABC acquiert à la fois des degrés de vitesse en nombre illimité (par la Proposition 10, partie II), donc (par l'Axiome 16), elle a réellement des parties différentes en nombre illimité.
C.Q.F.D.
(Lire les articles 34 et 35, partie II, des Principes.)
Scolie : Nous avons parlé jusqu'ici de la nature du mouvement ; il faut maintenant que nous en recherchions la cause qui est double ; savoir une cause première et générale qui est la cause de tous les mouvements qui sont dans le monde et une cause particulière par laquelle il arrive que les parties singulières de la matière acquièrent des mouvements qu'elles n'avaient pas auparavant. Pour ce qui touche la cause générale, comme nous ne devons rien admettre (par la Proposition 14 et le Scolie de la Proposition 17, partie I[3]) que nous ne percevions clairement et distinctement et que nous ne connaissons clairement et distinctement aucune autre cause que Dieu (c'est-à-dire le créateur de la Matière), il apparaît manifestement que nulle cause générale autre que Dieu ne doit être admise. Ce que, d'ailleurs, nous disons du mouvement devra s'entendre aussi du repos.
Proposition 12
Dieu est la cause principale du mouvement.
Démonstration : Voir le Scolie qui précède.
Proposition 13
La même quantité de mouvement et de repos que Dieu a imprimée une fois à la matière est conservée maintenant encore par son concours.
Démonstration : Comme Dieu est cause du mouvement et du repos (par la Proposition 12, partie II), il les conserve maintenant encore par la même puissance par laquelle il les a créés (par l'Axiome 10, partie I), et cela en la même quantité qu'il les a créés d'abord (par le Corollaire de la Proposition 20, partie I). C.Q.F.D.
Scolie : I. Bien que l'on dise dans la Théologie que Dieu fait beaucoup de choses par bon plaisir et pour montrer aux hommes sa puissance, comme ces choses qui dépendent de son bon plaisir ne sont pas connues sinon par révélation divine, elles ne devront pas être admises dans la Philosophie où il n'est recherché que ce qu'enseigne la Raison, afin que la Philosophie ne se confonde pas avec la Théologie.
II. Bien que le mouvement ne soit rien d'autre dans la matière mue, qu'un mode de cette matière, il a cependant une certaine quantité déterminée ; on verra par ce qui suit comment il faut l'entendre. Lire article 36, partie II, des Principes.
Proposition 14
Chaque chose, en tant qu'elle est simple et indivise, et qu'on la considère seulement en elle-même, persévère toujours, autant qu'il est en elle, dans le même état.
Cette Proposition est tenue par beaucoup pour un Axiome ; nous la démontrerons cependant.
Démonstration : Comme nulle chose n'est dans un certain état sinon par le seul concours de Dieu (par la Proposition 12, partie I) et que Dieu est constant au suprême degré dans ses œuvres (par le Corollaire de la Proposition 20, partie I), si nous n'avons égard à nulles causes extérieures, mais considérons une chose en elle seule, il faudra affirmer qu'autant qu'il est en elle, elle persévère toujours dans l'état où elle est. C.Q.F.D.
Corollaire : Un corps qui se meut une fois continue toujours à se mouvoir s'il n'est pas ralenti par des causes extérieures.
Démonstration : Elle suit clairement de la Proposition précédente ; toutefois pour corriger le préjugé relatif au mouvement, lire articles 37 et 38, partie II des Principes.
Proposition 15
Tout corps en mouvement tend de lui-même à continuer à se mouvoir suivant une ligne droite et non une ligne courbe.
On pourrait placer cette Proposition parmi les Axiomes ; je la démontrerai cependant par celles qui précédent.
Démonstration : Le mouvement, puisqu'il a Dieu seulement pour cause (par la Proposition 12, partie II), n'a par lui-même aucune force d'exister (par l'Axiome 10, partie I), mais il est à tout instant comme procréé par Dieu (par ce qui est démontré au sujet de l'Axiome sus-visé). Pour cette raison, aussi longtemps que nous avons égard à la seule nature du mouvement, nous ne pourrons jamais lui attribuer, comme appartenant à sa nature, une durée pouvant être plus grande qu'une autre. Or, si l'on disait qu'il appartient à la nature d'un corps en mouvement de décrire dans son mouvement une ligne courbe quelconque, on attribuerait à la nature du mouvement une durée plus grande que si l'on suppose qu'il est de la nature du corps mû de tendre à continuer de se mouvoir suivant une ligne droite (par l'Axiome 17). Or, comme (ainsi que nous l'avons déjà démontré) nous ne pouvons attribuer une telle durée à la nature du mouvement, il ne faut donc pas poser non plus qu'il est de la nature du corps mû de continuer à se mouvoir suivant aucune ligne courbe, mais seulement suivant une ligne droite. C.Q.F.D.
Scolie : Cette démonstration paraîtra peut-être à beaucoup ne pas montrer qu'il n'appartient pas à la nature du mouvement de décrire une ligne courbe et pas davantage qu'il lui appartient d'en décrire une droite ; et cela parce qu'on ne peut assigner aucune ligne droite, qu'il n'y ait une ligne plus petite, soit droite, soit courbe, et aucune ligne courbe qu'il n'y ait une ligne courbe plus petite. Cependant, même en tenant compte de cela, je juge que la démonstration n'en est pas moins correcte, puisqu'elle conclut de la seule essence universelle, c'est-à-dire de la différence essentielle des lignes (et non de la quantité de chacune d'elles, c'est-à-dire d'une différence accidentelle) ce qui était proposé à démontrer. Toutefois, pour ne pas rendre plus obscure en la démontrant une chose assez claire par elle-même, je renvoie les Lecteurs à la seule définition du mouvement, qui n'affirme rien du mouvement, sinon le transport d'une partie de la matière du voisinage, etc. dans le voisinage, etc. Par suite, à moins que nous ne concevions ce transport comme le plus simple possible, c'est-à-dire comme ayant lieu suivant une ligne droite, nous attribuerons, par fiction, au mouvement quelque chose qui n'est pas contenu dans sa définition ou son essence et ainsi n'appartient pas à sa nature.
Corollaire : Il suit de cette Proposition que tout corps qui se meut suivant une ligne courbe est continûment détourné de la ligne suivant laquelle de lui-même il continuerait à se mouvoir, et cela par la force de quelque cause extérieure (par la Proposition 14, partie II).
Proposition 16
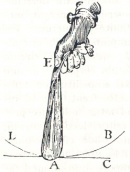
Tout corps qui est mû circulairement, comme par exemple une pierre dans une fronde, est constamment déterminé à continuer de se mouvoir suivant la tangente.
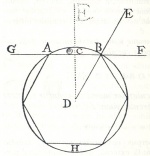
Démonstration : Un corps qui est mû circulairement est constamment empêché par une force extérieure de continuer à se mouvoir suivant une ligne droite (par le Corollaire de la Proposition précédente) ; si cette action venait à s'interrompre le corps continuerait de lui-même à se mouvoir suivant une ligne droite (par la Proposition 15). Je dis, en outre, qu'un corps qui est mû circulairement est déterminé par une cause extérieure à se mouvoir selon la tangente. Si on le nie, en effet, qu'on suppose, par exemple, en B une pierre déterminée par une fronde à se mouvoir non suivant la tangente BD, mais suivant une autre droite partant du même point et comprise ou non comprise dans le cercle, soit BF quand la fronde viendra de L vers B ; ou BG (que je connais qui fait avec le diamètre BH un angle égal à l'angle FBH) si au contraire on suppose que la fronde vient de C en B Si la pierre est au point B supposée déterminée par la fronde allant de L en B à continuer de se mouvoir vers F, il est nécessaire (par l'Axiome 18) quand la fronde par une détermination opposée viendra de C vers B, que la pierre soit déterminée à continuer de se mouvoir suivant la même ligne droite et, par suite, vers K non vers G, ce qui est contre l'hypothèse. Et comme[4] aucune ligne pouvant être menée par le point B, sauf la tangente, ne peut être supposée faire avec la ligne B deux angles égaux comme DBH et ABH, aucune ligne autre que la tangente ne peut s'accorder avec l'hypothèse, soit que la fronde aille de L en B ou de C en B ; et, par suite, on ne peut admettre d'autre ligne suivant laquelle la pierre puisse tendre à se mouvoir.C.Q.F.D.
Autre Démonstration : Soit conçu à la place d'un cercle un hexagone ABH inscrit dans un cercle et un corps C au repos en l'un des côtés AB de l'hexagone ; soit ensuite une règle DBE (dont je suppose une extrémité fixe au centre D, et l'autre mobile) se mouvant autour du centre D et coupant constamment la ligne AB. Il est clair que, si la règle DBE, tandis qu'elle se meut ainsi rencontre le corps C, au moment où elle coupe à angle droit la ligne AB, cette règle détermine par sa poussée le corps C à continuer de se mouvoir vers G suivant la ligne FBAG, c'est-à-dire suivant le côté AB de l'hexagone indéfiniment prolongé. Mais puisque nous avons choisi un hexagone arbitrairement on pourra affirmer la même chose de toute figure supposée inscrite dans le cercle, c'est-à-dire que, lorsque le corps C, au repos un certain instant sur l'un des côtés de la figure, est poussé par la règle DBE au moment où elle coupe ce côté à angle droit, il est déterminé par cette règle à se mouvoir selon le prolongement de ce côté. Concevons donc au lieu de l'hexagone une figure rectiligne d'un nombre infini de côtés (c'est-à-dire un cercle suivant la définition d'Archimède), il est clair que la règle DBE, quelque part qu'elle rencontre le corps C, le rencontrera toujours à un moment où elle coupe à angle droit un côté de la figure ; et ainsi elle ne rencontrera jamais le corps C sans le déterminer en même temps à se mouvoir selon ce côté indéfiniment prolongé. Et comme ce côté quelconque, prolongé dans l'un ou l'autre sens doit toujours tomber en dehors de la figure, il sera tangent à la figure d'un nombre infini de côtés, c'est-à-dire au cercle. Si donc au lieu d'une règle nous concevons une fronde mue circulairement, elle déterminera constamment la pierre à continuer de se mouvoir suivant une tangente.Il est à noter ici que l'une et l'autre démonstrations s'appliquent à des figures curvilignes quelconques.
Proposition 17
Tout corps qui est mû circulairement tend à s'éloigner du centre du cercle qu'il d'écrit.
Démonstration : Aussi longtemps qu'un corps quelconque est mû circulairement, il est contraint par une cause extérieure, et sitôt que cette action vient à cesser, il continue de se mouvoir suivant une tangente (par la Proposition précédente) dont tous les points, sauf le point de contact, tombent en dehors du cercle (par la Proposition 16 du Livre III des Éléments) et, par suite, sont plus éloignés du centre. Donc, quand une pierre qui est mue circulairement dans une fronde EA est au point A elle tend à continuer selon une ligne dont tous les points sont plus distants du centre E que tous ceux de la circonférence LAB, ce qui n'est pas autre chose que tendre à s'éloigner du centre du cercle qu'elle décrit.C.Q.F.D.
Proposition 18
Si un corps, disons A, se meut vers un corps immobile, B, B ne perd cependant rien de son repos par le choc du corps A et A non plus ne perd rien de son mouvement, mais retient entièrement la même quantité de mouvement qu'il avait auparavant.
Démonstration : Si on le nie, qu'on suppose que le corps A perd de son mouvement et ne transporte pas dans un autre, disons B, ce qu'il a perdu ; il y aura dans la Nature, quand cela arrivera, une quantité de mouvement moindre qu'auparavant, ce qui est absurde (par la Proposition 13, partie II). La démonstration procède de même à l'égard du repos dans le corps B ; c'est pourquoi si l'un ne le transporte pas dans l'autre, B conservera tout son repos et A tout son mouvement.C.Q.F.D.
Proposition 19
Le mouvement considéré en lui-même diffère de sa détermination à suivre telle ou telle direction et il n'est pas nécessaire qu'un corps mû, pour être porté dans la direction opposée ou repoussé, soit quelque temps au repos.
Démonstration : Qu'on suppose comme dans la Proposition précédente que le corps A se meuve vers le corps B et soit empêché par B de continuer son mouvement, il conservera donc la totalité de son mouvement (par la Proposition précédente) et ne restera pas immobile le plus petit espace de temps ; toutefois, quand il continuera de se mouvoir, il ne se mouvra pas dans la même direction où il se mouvait auparavant, car on suppose qu'il en est empêché par B ; donc son mouvement se conservant entièrement et la détermination antérieure étant perdue il se mouvra dans la direction opposée (par ce qui est dit au Chapitre II de la Dioptrique) et ainsi (par l'Axiome 2) la détermination à suivre une certaine direction n'appartient pas à l'essence du mouvement, mais en diffère et le corps mû, quand il est repoussé, n'est en repos aucun moment. C.Q.F.D.
Corollaire : Il suit de là que le mouvement n'est pas opposé au mouvement.
Proposition 20
Si un corps A rencontre un corps B et l'entraîne avec lui, A perd de son mouvement autant que B en acquiert de A à la suite du choc de A.
Démonstration : (Voir la figure 1.) Si on le nie supposons que B acquiert de A plus ou moins de mouvement que A n'en perd ; toute la différence devra être ajoutée à la quantité de mouvement de la Nature entière ou en devra être retranchée ce qui est absurde (par la Proposition 13, partie II). Donc, comme le corps B ne peut acquérir ni plus ni moins de mouvement que n'en perd A, il en acquerra tout juste autant. C.Q.F.D.
Proposition 21
Si un corps A est deux fois plus grand qu'un corps B et se meut avec une vitesse égale, A aura un mouvement double de B, c'est-à-dire la force de garder la même vitesse que B. (Voir la figure 1).
Démonstration : Qu'on pose par exemple à la place de A deux fois B, c'est-à-dire (par hypothèse) le seul A divisé en deux parties égales, les deux B auront la force de rester dans l'état où ils sont (par la Proposition 14, partie II), et cette force est égale dans les deux (par hypothèse). Si maintenant ces deux B sont joints, on aura un seul A dont la force et la quantité seront égales aux deux B, c'est-à-dire doubles d'un seul B. C.Q.F.D.
On notera que cela découle aussi de la seule définition du mouvement ; plus en effet le corps qui se meut est grand, plus il y a de matière qui est séparée d'une autre quantité de matière, et il y a donc plus de séparation, c'est-à-dire (par la Définition 8) plus de mouvement. Voir notre 4° Observation sur la définition du mouvement.
Proposition 22
Si un corps A est égal à un corps B et que A se meuve deux fois plus vite que B, la force ou le mouvement sera en A double de B.
Démonstration : Supposons que B, quand il a acquis une certaine force de se mouvoir, ait acquis quatre degrés de vitesse. Si rien ne survient, il continuera de se mouvoir (par la Proposition 14, partie II) et de persévérer dans son état. Supposons maintenant qu'il acquière par une nouvelle impulsion une nouvelle force égale à la première ; il acquerra donc quatre nouveaux degrés en sus des quatre premiers qu'il conservera (par la même Proposition), c'est-à-dire qu'il se mouvra deux fois plus vite, soit avec une vitesse égale à celle de A, et en même temps il aura une force double, c'est-à-dire égale à celle de A ; donc le mouvement est en A double de B.
On observera que nous entendons ici par force dans les corps en mouvement une quantité de mouvement, quantité qui dans des corps égaux doit être plus grande à proportion de la rapidité du mouvement, en tant que par cette vitesse des corps égaux sont séparés de ceux qui leur sont immédiatement contigus plus qu'ils ne seraient au même instant s'ils se mouvaient plus lentement ; et par là (par la Définition 8) ont aussi plus de mouvement. Dans les corps au repos on entend pas force de résister une quantité de repos. D'où il suit :
Corollaire 1 : Plus les corps se meuvent lentement, plus ils participent du repos, car aux corps mûs plus rapidement qui les rencontrent et qui ont une force moindre qu'eux-mêmes, ils résistent davantage et ils sont aussi moins séparés de ceux qui les touchent immédiatement.
Corollaire 2 : Si un corps A se meut deux fois plus vite qu'un corps B et que B soit deux fois plus grand que A, il y a autant de mouvement en B, le plus grand des deux, qu'en A, le plus petit, et par conséquent aussi une force égale.
Démonstration : Soit B deux fois plus grand que A, A se mouvant deux fois plus vite que B, et ensuite C deux fois plus petit que B et deux fois plus lent que A ; B aura donc (par la Proposition 21 partie II) un mouvement double de C et A (par la Proposition 22, partie II) un mouvement double de C ; donc (par l'Axiome 15) B et A auront des mouvements égaux, car le mouvement de chacun d'eux est double du même troisième C. C.Q.F.D.
Corollaire 3 : Il suit de là, que le mouvement est distinct de la vitesse. Nous concevons en effet que de deux corps ayant même vitesse l'un puisse avoir plus de mouvement que l'autre (par la Proposition 21, partie II) ; et inversement qu'ayant des vitesses inégales ils puissent avoir des mouvements égaux (par le corollaire précédent). Cela ressort d'ailleurs aussi de la seule définition du mouvement qui n'est pas autre chose que le transport d'un corps du voisinage, etc.
Il faut noter toutefois que ce troisième corollaire ne contredit pas le premier. Car la vitesse est conçue par nous de deux façons ; ou bien en tant qu'un corps est séparé plus ou moins au même instant des corps le touchant immédiatement et, comme tel, participe plus ou moins du mouvement ou du repos ; ou bien en tant qu'il parcourt en un même temps une distance plus grande ou plus petite et à cet égard est distinct du mouvement.
J'aurais pu ajouter ici d'autres Propositions pour développer plus amplement la Proposition 14 de cette partie et expliquer les forces des choses en un état quelconque, comme nous l'avons fait ici à l'égard du mouvement ; mais il suffira de lire l'Article 43, partie II des Principes, et d'adjoindre seulement une Proposition qui est nécessaire pour entendre ce qui suit.
Proposition 23
Quand les modes d'un corps doivent éprouver un changement, ce changement est toujours le moindre qui puisse être.
Démonstration : Cette Proposition découle assez clairement de la Proposition 14 de cette Partie.
Proposition 24 - Règle 1
Si deux corps, disons A et B (voir la figure 1), sont tout à fait égaux et qu'ils se meuvent en ligne droite l'un vers l'autre avec une égale vitesse, quand ils se rencontreront l'un l'autre, chacun rejaillira du côté opposé sans perdre aucune partie de sa vitesse.
Dans cette hypothèse il est clair que, pour supprimer l'opposition des deux corps, il faut ou que l'un et l'autre soient renvoyés du côté opposé ou que l'un entraîne l'autre avec lui ; car ils sont opposés quant à la détermination à suivre une direction, mais non quant au mouvement.
Démonstration : Quand A et B se rencontrent l'un l'autre, ils doivent éprouver un certain changement (par l'Axiome 19) ; comme d'ailleurs le mouvement n'est pas opposé au mouvement (par le Corollaire de la Proposition 19, partie II), ils ne doivent rien perdre de leur mouvement (par l'Axiome 19). C'est pourquoi le changement aura lieu dans la direction seulement ; mais nous ne pouvons concevoir que la direction de l'un seulement, soit B, soit changée à moins de supposer A, qui devrait produire ce changement, plus fort que B (par l'Axiome 20). Mais cela serait contre l'hypothèse. Donc, puisqu'un changement de direction ne peut pas avoir lieu seulement dans l'un, il aura lieu dans l'un et l'autre, c'est-à-dire que A et B seront renvoyés du côté opposé (par ce qui est dit au chapitre II de la Dioptrique) et garderont la totalité de leur mouvement.
Proposition 25 - Règle 2
Si les corps sont inégaux en volume, à savoir B plus grand que A (voir figure 1), les autres conditions étant supposées les mêmes que précédemment, alors A seulement rejaillira et les deux corps continueront à se mouvoir avec la même vitesse.
Démonstration : Puisque A est supposé plus petit que B, il aura aussi (par la Proposition 21, partie II) une force moindre ; or, puisque dans cette hypothèse comme dans la précédente il n'y a d'opposition que dans la seule direction et qu'ainsi, comme nous l'avons démontré dans la Proposition précitée, il ne doit y avoir de changement que dans la seule direction, il ne s'en produira qu'en A et non en B (par l'Axiome 20) ; donc A seulement sera renvoyé du côté opposé par B qui est plus fort, en gardant sa vitesse entière. C.Q.F.D.
Proposition 26
Si des corps sont inégaux par le volume et la vitesse à savoir B deux fois plus grand que A (voir la figure 1), mais le mouvement en A deux fois plus rapide qu'en B, les autres conditions étant supposées les mêmes que précédemment, tous deux rejailliront du côté opposé, chacun gardant la vitesse qu'il avait.
Démonstration : Puisque A et B se meuvent l'un vers l'autre selon l'hypothèse, il y a autant de mouvement dans l'un que dans l'autre (par le Corollaire de la Proposition 22, partie II) : donc le mouvement de l'un n'est pas contraire au mouvement de l'autre (par le Corollaire de la Proposition 19, partie II) ; et les forces sont égales dans l'un et l'autre (par le Corollaire 2 de la Proposition 22, partie II). Cette hypothèse est ainsi entièrement semblable à celle de la Proposition 24 ci-dessus ; et ainsi, par la même démonstration, A et B rejailliront en sens contraire en gardant leur mouvement en entier. C.Q.F.D.
Corollaire : Des trois Propositions précédentes il suit clairement que la direction d'un corps requiert, pour être changée, la même force que le mouvement ; d'où suit qu'un corps qui perd plus de la moitié de sa détermination à suivre une direction et plus de la moitié de son mouvement, éprouve plus de changement que celui qui perd la totalité de sa détermination.
Proposition 27 - Règle 3
Si des corps sont égaux en volume, mais que B se meuve un peu plus vite que A, non seulement A rejaillira du côté opposé, mais B transportera dans A la moitié de l'excès de vitesse qu'il a sur A et tous deux continueront de se mouvoir du même côté. (voir la figure 1)
Démonstration : A (par hypothèse) n'est pas seulement opposé à B par sa direction, mais aussi par sa lenteur en tant que celle-ci participe du repos (par le Corollaire de la Proposition 22, partie II). Par suite, s'il est renvoyé du côté opposé et que seule sa direction soit changée, toute opposition n'est pas détruite pour cela entre ces deux corps, donc (par l'Axiome 19) il doit y avoir changement et dans la direction et dans le mouvement. Mais comme, par hypothèse, B se meut plus vite que A, B (par la Proposition 22, partie II) sera plus fort que A, donc (par l'Axiome 20) un changement sera produit en A par B, par qui A sera renvoyé du côté opposé. Ce qui était le premier point.
Maintenant, aussi longtemps que A se meut plus lentement que B il est opposé à B (par le Corollaire de la Proposition 22, partie II), donc le changement doit se poursuivre (par l'Axiome 19) jusqu'à ce que A ne se meuve pas plus lentement que B. Mais il n'est pas dans l'hypothèse examinée de cause assez forte pour le faire se mouvoir plus vite que B ; puis donc qu'il ne peut se mouvoir ni plus lentement que B, alors qu'il est poussé par B, ni plus vite que B, il continuera à se mouvoir avec la même vitesse que B. En outre, si B transporte dans A moins de la moitié de son excès de vitesse, A se mouvra moins vite que B ; si B transporte plus de la moitié de cet excès, alors A se mouvra plus vite que B ; l'un et l'autre sont absurdes, comme nous l'avons déjà démontré. Donc le changement se poursuivra jusqu'à ce que B ait fait passer dans A la moitié de son excès de vitesse que (par la Proposition 20, partie II) il doit perdre ; et ainsi tous deux continueront à se mouvoir du même côté et également vite sans plus d'opposition entre eux. C.Q.F.D.
Corollaire : Il suit de là que plus un corps se meut vite, plus il est déterminé à se mouvoir suivant la ligne qu'il parcourt, et au contraire, plus lentement il se meut, moins il a de détermination à suivre une certaine direction.
Scolie :
Pour que les Lecteurs ne confondent pas ici la force de détermination avec la force du mouvement, il a paru bon d'ajouter quelques observations établissant clairement la distinction de ces deux forces. Si donc l'on conçoit deux corps égaux A et C se mouvant directement l'un vers l'autre avec des vitesses égales, ces deux corps (par la Proposition 24, partie II) rejailliront du côté opposé en gardant tout leur mouvement. Mais, si le corps C est en B et se meut obliquement vers A, il est clair qu'il a une détermination moindre à se mouvoir suivant la ligue BD ou CA. Donc, bien qu'il ait autant de mouvement que A, la force de détermination de C se mouvant directement vers A, qui est égale à la force de déterminations du corps A, est plus grande que la force de détermination du même C se mouvant de B vers A ; et d'autant plus grande quel la ligne BA est plus grande que la ligne CA ; car plus la ligne BA l'emporte en grandeur sur la ligne CA, plus il est requis de temps (le corps situé en B et A étant supposés ici se mouvoir avec la même vitesse) pour que le corps situé en B puisse se mouvoir suivant la ligne BD ou CA par laquelle il est opposé à la direction de A. Et ainsi, quand C venant de B rencontre A obliquement, il est déterminé tout de même que s'il devait continuer à se mouvoir vers B’ suivant la ligne AB (B’ étant un point de la ligne BC prolongée situé à la même distance de C que B). A cependant, gardant tout son mouvement et toute sa détermination, continuera à se mouvoir vers C et poussera avec lui le corps situé d'abord en B ; puisque ce corps, aussi longtemps qu'il est déterminé à se mouvoir suivent la diagonale AB’ et se meut avec la même vitesse que A, a besoin de plus de temps pour décrire une partie quelconque de la ligne AC et est opposé en cela même à la détermination plus forte de A. Mais, pour que la force de détermination de C se mouvant de B vers A soit égale à la force de détermination du même C se mouvant directement vers A (force égale par hypothèse à celle de A), il est nécessaire que le corps situé en B ait autant de degrés de mouvement de plus que le corps A, que la ligne BA a de longueur de plus que la ligne CA et alors, quand ce corps rencontrera le corps A obliquement, il sera renvoyé vers B’ dans une direction opposée à celle qu'il suivait et A vers A’ l'un et l'autre gardant tout leur mouvement. Par contre, si l'excès de mouvement du corps situé en B l'emporte sur l'excès de longueur de la ligne BA sur la ligne CA, alors ce corps repoussera A vers A’ et lui communiquera une partie de son mouvement jusqu'à ce que l'égalité des deux excès s'établisse (c'est-à-dire qu'il y ait entre les mouvements des deux corps le même rapport qu'entre les lignes BA et CA), perdant lui-même autant de mouvement qu'il en cède et continuera à se mouvoir du même côté qu'avant la rencontre. Par exemple, si la ligne AC est à AB comme 1 à 2 et le mouvement du corps A à celui du corps situé en B comme 1 à 5, ce dernier corps transportera dans A un degré de son mouvement, le repoussera du côté opposé et continuera lui-même à se mouvoir dans la direction qu'il suivait avec quatre degrés de mouvement.Proposition 28 - Règle 4
Si un corps A (voir figure 1) est complètement au repos, et un peu plus grand que le corps B, avec quelque vitesse que B se meuve vers A, jamais il ne mettra A en mouvement mais sera repoussé par lui du côté opposé gardant tout son mouvement.
On observera que l'opposition de ces corps peut être détruite de trois manières : ou bien quand l'un d'eux entraîne l'autre avec lui et qu'ils continuent ensuite a se mouvoir du même côté avec la même vitesse ; ou bien quand l'un est renvoyé du côté opposé et que l'autre garde tout son repos ; ou bien quand l'un est renvoyé du côté opposé et transfère une partie de son mouvement à l'autre qui est au repos ; il n'y a pas de quatrième cas (en vertu de la Proposition 13, partie II). Il y aura donc à démontrer maintenant (à cause de la Proposition 23, partie II) que dans notre hypothèse le changement qui se fait dans ces corps est le plus petit qui se puisse.
Démonstration : Si B mettait A en mouvement, il devrait (par la Proposition 20, partie II), jusqu'au moment où les deux corps se mouvraient avec la même vitesse, céder à A autant de mouvement que A en acquerrait et (par la Proposition 21, partie II) il devrait perdre plus de la moitié de son mouvement et conséquemment aussi (par le Corollaire de la Proposition 27, partie II) plus de la moitié de sa détermination ; et ainsi (par le Corollaire de la Proposition 26, partie II) il éprouverait plus de changement que s'il perdait seulement sa détermination. Et, si A perd quelque chose de son repos, mais non assez pour pouvoir continuer de se mouvoir avec la même vitesse que B, alors l'opposition des deux corps n'est pas détruite ; car A s'opposera par sa lenteur, en tant qu'elle participe du repos (par le Corollaire de la Proposition 22, partie II), à la vitesse de B et ainsi B devra encore être renvoyé du côté opposé et perdra avec toute sa détermination la partie de son mouvement qu'il aura fait passer en A, ce qui est un changement plus grand que s'il perdait seulement sa détermination. Le changement donc, dans notre hypothèse, sera, parce qu'il n'a lieu que dans la seule détermination, le plus petit qui puisse être dans ces corps, et par conséquent (par la Proposition 23, partie II) aucun autre ne se produira. C.Q.F.D.
On notera dans la démonstration de cette Proposition que la même chose a lieu aussi dans d'autres cas ; nous n'avons pas en effet cité la Proposition 19, partie II, dans laquelle il est démontré, que la direction peut être entièrement changée, le mouvement subsistant cependant en entier ; il faut cependant y avoir égard pour que la force de la démonstration soit bien perçue. Car, dans la Proposition 23, partie II, nous ne disions pas que le changement doit être le plus petit absolument, mais le plus petit qui puisse être.
Qu'un changement consistant dans la seule détermination tel que celui que nous avons supposé dans cette démonstration puisse avoir lieu, cela se voit par les Propositions 18 et 19, partie II, avec le Corollaire.
Proposition 29 - Règle 5
Si un corps A au repos (voir figure 1) est plus petit que B, si lentement que B se meuve vers A, il le mettra en mouvement avec lui, lui transférant une partie de son mouvement telle que tous deux ensemble se meuvent ensuite également vite (Lire Article 50, partie II, des Principes).
Dans cette règle comme dans la précédente on peut concevoir trois cas seulement dans lesquels l'opposition est détruite : nous démontrerons que dans notre hypothèse ce changement qui se fait dans ces corps est le plus petit qui se puisse, et ainsi (par la Proposition 23, partie II) que c'est celui-là qui doit se faire.
Démonstration : Dans notre hypothèse B transporte dans A (par la Proposition 21, partie II) moins de la moitié de son mouvement et (par le Corollaire de la Proposition 26, partie II[5]) moins de la moitié de sa détermination. Or, si B n'entraînait pas A avec lui mais était renvoyé du côté opposé, il perdrait toute sa détermination et le changement serait plus grand (par le Corollaire de la Proposition 26, partie II) ; et bien plus grand encore si B perdait toute sa détermination et en même temps une partie de son mouvement comme on le suppose dans ce troisième cas ; donc, dans notre hypothèse, le changement est le plus petit possible. C.Q.F.D.
Proposition 30 - Règle 6
Si un corps A au repos, était rigoureusement égal à un corps B se mouvant vers lui, il serait en partie poussé par lui et en partie le repousserait du côté opposé. (voir figure 1)
Ici encore comme dans la Proposition précédente, trois cas seulement peuvent être conçus ; il faut donc montrer que le changement supposé par nous est le plus petit qui se puisse.
Démonstration : Si le corps B entraîne avec lui le corps A, jusqu'à ce que tous deux se meuvent avec la même vitesse, il y aura alors autant de mouvement dans l'un que dans l'autre (par la Proposition 22, partie II) et (par le Corollaire de la Proposition 27, partie II) B devra perdre la moitié de sa détermination et aussi (par la Proposition 20, partie II) la moitié de son mouvement. Si, au contraire, il est repoussé par A du côté opposé, alors il perdra sa détermination en entier et gardera son mouvement (par la Proposition 18, partie II), changement égal au précédent. Mais ni l'un ni l'autre ne peut être ; car si A gardait son état et pouvait changer la détermination de B, il devrait être nécessairement (par l'Axiome 20) plus fort que B, ce qui serait contre l'hypothèse. Et, si B entraînait A avec lui jusqu'à ce que tous deux se mussent avec la même vitesse, B serait plus fort que A, ce qui est aussi contre l'hypothèse. Puis donc que ni l'un ni l'autre de ces deux cas n'est possible, c'est donc le troisième qui se produira, à savoir que B poussera A un peu et sera repoussé par A. C.Q.F.D.
Lire Article 51, partie II, des Principes.
Proposition 31 - Règle 7
Si B et A se mouvaient dans la même direction, A plus lentement mais B le suivant plus vite, de telle façon qu'il l'atteignît enfin, et que A fût plus grand que B mais que l'excès de vitesse en B fût plus grand que l'excès de grandeur en A, B alors fera passer en A une partie de son mouvement telle que tous deux ensuite s'avancent avec la même vitesse et dans la même direction. Si par contre l'excès de grandeur en A était plus grand que l'excès de vitesse en B, B serait repoussé dans la direction opposée en gardant tout son mouvement.(voir figure 1)
Lire article 52, partie II des Principes. Ici encore trois cas seulement peuvent être conçus.
Démonstration : Première partie. — B ne peut pas être renvoyé dans la direction opposée par A, puisqu'il est (par les Propositions 21 et 22, partie II) supposé plus fort que A ; donc B étant le plus fort, il entraîne A avec lui, et cela de telle façon que les deux continuent à se mouvoir avec la même vitesse. Alors le changement sera le plus petit possible, comme il se voit facilement par ce qui précède.
Deuxième partie. — B ne peut, étant supposé moins fort que A (par les Propositions 21 et 22, partie II), pousser A ni lui céder aucune partie de son mouvement (par l'Axiome 20), donc (par le Corollaire de la Proposition 14, partie II) il retiendra tout son mouvement mais ne se mouvra pas du même côté puisqu'il en est, par hypothèse, empêché par A ; donc (par ce qui est dit au chapitre II de la Dioptrique) il sera renvoyé (par la Proposition 18, partie II) du côté opposé en gardant tout son mouvement. C.Q.F.D.
On observera que dans cette Proposition et dans les précédentes nous avons tenu pour démontré que tout corps en rencontrant un autre directement et absolument empêché par lui de continuer à avancer du même côté doit rejaillir du côté opposé et non dans aucune autre direction ; pour le bien entendre, lire le chapitre II de la Dioptrique.
Scolie : Nous avons jusqu'ici, pour expliquer les changements résultant de la rencontre, considéré les deux corps comme entièrement séparés de tous autres corps, sans avoir le moindre égard aux corps qui les entourent de toutes parts. Maintenant nous considérerons l'état et les changements en tenant compte des corps environnants.
Proposition 32
Si un corps B est entouré de toutes parts de petits corps en mouvement le poussant avec la même force dans toutes les directions, aussi longtemps qu'aucune autre cause n'intervient, il restera immobile au même lieu.
Démonstration : Cette Proposition est évidente par elle-même ; si, en effet, le corps était mû dans une direction quelconque par l'impulsion des corpuscules venant d'un certain côté, les corpuscules qui le mettraient en mouvement le pousseraient avec une force plus grande que ceux qui, au même instant, le poussent du côté opposé et ne peuvent avoir leur effet (par l'Axiome 20), ce qui serait contre l'hypothèse.
Proposition 33
Le corps B, dans les conditions ci-dessus, peut, par la survenue d'une force aussi petite qu'on voudra, être mû dans une direction quelconque.
Démonstration : Tous les corps touchant B immédiatement, puisque (par hypothèse) ils sont en mouvement et que B (par la Proposition précédente) reste immobile, sitôt qu'ils touchent B rejailliront du côté opposé en gardant tout leur mouvement (par la Proposition 28, partie II) ; et ainsi le corps B est constamment délaissé par les corps qui le touchent immédiatement ; si grand que l'on veuille supposer B, aucune action n'est donc requise pour le séparer des corps qui le touchent immédiatement (par notre quatrième observation au sujet de la Définition 8). Donc aucune force extérieure, si petite qu'on la veuille supposer, ne peut être appliquée à B, qu'elle ne soit plus grande que la force par laquelle B demeure dans le même lieu (car nous l'avons déjà démontré, il n'a lui-même aucune force de rester attaché aux corps le touchant immédiatement) ; et plus grande aussi, jointe à l'impulsion des corpuscules poussant B du même côté qu'elle, que la force des corpuscules poussant B du côté opposé (et supposée égale à l'impulsion contraire) ; donc (par l'Axiome 20), le corps B sera mis en mouvement par cette force extérieure si petite qu'elle soit. C.Q.F.D.
Proposition 34
Le corps B dans les mêmes conditions que ci-dessus ne peut être mû plus rapidement que ne le pousse la force extérieure encore que les particules, dont il est entouré, soient agitées d'un mouvement beaucoup plus rapide.
Démonstration : Les corpuscules qui, en même temps que la force extérieure, poussent le corps B d'un certain côté, bien qu'agités d'un mouvement beaucoup plus rapide que l'impulsion donnée à B par la force extérieure, n'ont toutefois point (par hypothèse), une force plus grande que les corpuscules poussant B du côté opposé ; et, par suite, dépenseront à résister seulement à ces derniers toutes leurs forces de détermination et ne conféreront à B (par la Proposition 32, partie II), aucune vitesse. Donc, puisqu'on ne suppose pas d'autres circonstances ni d'autres causes, B ne recevra de vitesse d'aucune autre cause que de la force extérieure et par conséquent (par l'Axiome 8, partie I) ne pourra être mû plus rapidement que ne le pousse la force extérieure. C.Q.F.D.
Proposition 35
Quand un corps B est ainsi mû par une force extérieure, il reçoit la plus grande partie de son mouvement des corps dont il est constamment entouré, et non de la force extérieure.
Démonstration : Le corps B, quelque grand qu'on le suppose, doit être mû par une impulsion si petite qu'elle soit (par la Proposition 33, partie II).
Concevons donc le corps B quatre fois plus grand que le corps extérieur par la force duquel il est poussé ; puis donc que (par la Proposition précédente) tous deux doivent se mouvoir également vite, il y aura quatre fois plus de mouvement en B que dans le corps extérieur qui le pousse (par la Proposition 21, partie II) ; ce n'est donc pas (par l'Axiome 8, partie I) de la force extérieure qu'il tient la partie principale de son mouvement. Et, puisqu'on ne suppose point d'autres causes que les corps dont il est constamment entouré (le corps B est en effet supposé immobile de lui-même) il reçoit donc (par l'Axiome 7, partie I) des seuls corps dont il est entouré et non de la force extérieure, la partie principale de son mouvement. C.Q.F.D.
On observera que nous ne pouvons ici dire comme ci-dessus que ce mouvement des particules venant d'un côté est requis pour résister au mouvement des particules venant du côté opposé ; car les corps se mouvant les uns vers les autres avec un mouvement égal (comme il est supposé ici) sont opposés par la détermination [6] seulement, non par le mouvement (par le Corollaire de la Proposition 19, partie II) et donc dépensent en résistant les uns aux autres leur détermination seulement et non leur mouvement ; c'est pourquoi le corps B ne peut recevoir des corps qui l'environnent aucune détermination et conséquemment aucune vitesse (par le Corollaire de la Proposition 27, partie II) en tant que la vitesse est distincte du mouvement, mais il en reçoit du mouvement, bien plus à la survenue d'une force additionnelle il doit être mû par eux comme nous l'avons démontré dans cette Proposition et comme on le voit clairement par la manière dont nous avons démontré la Proposition 33.
Proposition 36
Si un corps, par exemple notre main, peut être mue d'un certain mouvement égal dans toute direction, de façon qu'elle ne résiste, en aucune façon, à aucuns corps et qu'aucuns corps ne lui résistent en aucune façon, il est nécessaire que dans l'espace où elle se meut ainsi il y ait autant de corps mûs d'un côté que d'un autre quelconque avec une force de vitesse égale à celle de la main.
Démonstration : Un corps ne peut se mouvoir en aucun espace qui ne soit plein de corps (par la Proposition 3, partie II). Je dis donc que l'espace dans lequel notre main peut se mouvoir ainsi est plein de corps qui se meuvent dans les conditions que j'ai dites. Si on le nie, qu'on suppose qu'ils soient au repos ou se meuvent d'une autre façon. S'ils sont au repos ils résisteront nécessairement au mouvement de la main (par la Proposition 14, partie II) jusqu'à ce que ce mouvement leur ait été communiqué de façon qu'ils se meuvent du même côté qu'elle avec une vitesse égale à la sienne (par la Proposition 20, partie II). Mais dans notre hypothèse ils ne résistent pas ; donc ces corps sont en mouvement, ce qui était le premier point.
Maintenant ils doivent se mouvoir de tous les côtés. Si on le nie, qu'on suppose un côté duquel ils ne se meuvent pas, disons de A vers B. Si alors la main se meut de A en B, elle rencontrera nécessairement des corps en mouvement (par la première partie de cette démonstration) et, suivant l'hypothèse que l'on vient de faire, avec une détermination différente de celle de la main ; ils lui résisteront donc (par la Proposition 14, partie II) jusqu'à ce qu'il soient mûs du même côté que la main (par la Proposition 24 et le Scolie de la Proposition 27, partie II). Or, ces corps (par hypothèse) ne résistent pas à la main ; donc ils se meuvent dans toutes les directions possibles, ce qui était le second point.
Je dis maintenant que ces corps se mouvront de tous les côtés avec la même force de vitesse. Supposons en effet qu'il n'en soit pas ainsi et que ceux qui se meuvent de A vers B aient une force de vitesse moindre que ceux qui se meuvent de A vers C. Alors, si la main était mue de A vers B avec la même vitesse que sont mus les corps allant de A vers C (elle est supposée en effet pouvoir être mue d'un mouvement égal de tous les côtés sans résistance) les corps allant de A vers B résisteraient au mouvement de la main (par la Proposition 14, partie II) jusqu'à ce qu'ils se mussent avec la même force de vitesse qu'elle-même (par la Proposition 31, partie II). Mais cela est contre l'hypothèse ; donc les corps se mouvront avec la même force de vitesse de tous les côtés, ce qui était le troisième point.Enfin, si les corps se mouvaient avec une force de vitesse inégale à celle de la main, ou bien la main se mouvra plus lentement, c'est-à-dire avec une force de vitesse moindre que les corps, ou bien elle se mouvra plus vite, c'est-à-dire avec une force de vitesse plus grande. Dans le premier cas, la main résistera aux corps la suivant dans la même direction (par la Proposition 31, partie II). Dans le second cas, les corps que suit la main en allant dans la même direction lui résisteront (par la même Proposition). L'une et l'autre conséquence sont contre l'hypothèse. Donc puisque la main ne peut se mouvoir ni plus lentement ni plus vite, elle se mouvra avec la même force de vitesse que les corps. C.Q.F.D.
Si l'on demande pourquoi je dis la même force de vitesse et non simplement la même vitesse, qu'on lise le Scolie du Corollaire de la Proposition 27, partie II. Si l'on me demande ensuite si la main allant par exemple de A vers B ne résiste pas aux corps se mouvant en même temps avec une force égale de B vers A, qu'on lise la Proposition 33, partie II, par où l'on comprendra que la force de ces corps est compensée par celle des corps qui se meuvent en même temps avec la main de A vers B (force qui, par la troisième partie de la démonstration ci-dessus, doit égaler la première).
Proposition 37
Si un corps, disons A, peut être mis en mouvement d'un côté quelconque par une force quelque petite qu'elle soit, il est nécessairement entouré de corps mûs avec une vitesse qui est la même pour tous.
Démonstration :
Le corps B doit être entouré de toutes parts de corps (par la Proposition 6, partie II) et de corps mûs également dans toutes les directions. Si en effet ces corps étaient au repos, A ne pourrait pas, comme il est supposé, être mû d'un côté quelconque par une force quelque petite qu'elle fût, mais ne pourrait l'être que par une force capable au moins de mouvoir avec elle les corps touchant A immédiatement (par l'Axiome 20, partie II). En outre, si les corps dont A est entouré étaient mûs par une force plus grande d'un côté que d'un autre, disons de B vers C que de C vers B, comme il est entouré de toutes parts de corps en mouvement (ainsi que nous l’avons déjà démontré), il arriverait nécessairement que les corps se mouvant de B vers C entraîneraient avec eux le corps A (par ce que nous avons démontré Proposition 33). Et ainsi une force, quelque petite qu'elle fût, ne suffirait pas à mouvoir A vers B, mais elle devrait être assez grande pour compenser l'excès de mouvement des corps venant de B vers C (par l'Axiome 20) ; donc les corps entourant A doivent se mouvoir avec une force égale de tous les côtés.C.Q.F.D.
Scolie : Comme ce que nous avons supposé se trouve advenir pour les corps appelés Fluides, il s'ensuit que les corps fluides sont ceux qui sont divisés en un grand nombre de petites particules mues avec une force égale de tous les côtés. Et bien que ces particules ne puissent être aperçues par aucun œil, fût-il d'un lynx, il ne faut cependant pas nier ce que nous avons démontré clairement. Car, par ce qui a été dit dans les Propositions 10 et 11, nous sommes déjà parvenus à établir une subtilité de la Nature telle que notre pensée (pour ne rien dire des sens) ne peut la délimiter ni l'atteindre. De plus, comme il est assez certain par ce qui précède que les corps résistent aux autres corps, par leur repos seulement, et que dans la dureté, ainsi que les sens l'indiquent, nous ne percevons rien d'autre sinon que les parties des corps durs résistent au mouvement de nos mains, nous concluons clairement que les corps durs sort ceux dont toutes les particules sont en repos les unes à l'égard des autres. Lire Articles 54, 55, 56, partie II des Principes.
Notes
- ↑ Voir, à ce sujet, de plus amples détails dans l’Appendice partie II, chap. III et IX.
- ↑ Voir la figure jointe à la Proposition suivante.
- ↑ *L'édition originale et la traduction de Balling, suivies en cela par Gebhardt, donnent cette référence à un scolie qui n'existe pas. On peut raisonnablement supposer qu'il s'agit d'une coquille pour « Scholie de la Proposition 15, partie I (Prop. 15 ejusd. Part.) ». (N.d.JF)
- ↑ Cela est évident par les proposition 18 et 19 du 3° livre des Éléments.
- ↑ Le texte original latin parle ici de la prop. 17 seulement, elle n'a pas de corollaire. ». (N.d.E.)
- ↑ Normal 0 21 false false false FR X-NONE X-NONE Voir la Proposition 24, partie II ; nous y avons démontré en effet que deux corps en résistant l'un à l'autre dépensent leur détermination, non leur mouvement.